El de hagamos un trato, la teoría de juegos y todos perdemos

Por si dejas de leer pronto,  empezaré por lo más divertido. Supongamos que nos vamos a un concurso de la tele, llegamos a la final y ésta consiste en el clásico juego de las tres puertas. Tras dos de ellas hay un borrego, tras la otra un coche. Como soy simple y no me gusta marearme, elijo la primera.  Pero entonces, el presentador  hace lo de siempre, me enseña que en la tercera puerta hay un borrego y me ofrece cambiar. ¿Qué debo hacer?

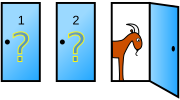¿Sigo con la 1 o me paso a la dos?

Este problema se conoce como la paradoja de Monty Hall, nombre del presentador del programa hagamos un trato (Let´s make a deal) en alguna tele de los americanos. Mi lógica inicial dice que tengo dos puertas, la uno y la dos, y por tanto,  un 50 % de posibilidades de ganar, ya me mueva o no. Pero en realidad, estoy perdiendo un dato importante, el presentador me ha revelado una información crucial. Hay dos cosas que el presentador no puede hacer: mostrarme lo que hay en mi puerta seguro,  y de las dos que quedan mostrarme la tenga el coche. Esto otorga a la puerta tres la parte de éxito de la puerta 2. Veamos los tres casos:

Caso	Puerta 1	Puerta 2	Puerta 3	Me quedo con 1	La cambio
Caso 1	Coche	Borrego	Borrego	Coche	Borrego
Caso 2	Borrego	Coche	Borrego	Borrego	Coche
Caso 3	Borrego	Borrego	Coche	Borrego	Coche

En el caso 2 y 3, el presentador no tiene alternativa, debe abrir la puerta 3 y la 2, respectivamente, porque no me puede enseñar el coche. Esto se llama, técnicamente, probabilidad condicionada. Una vez que ya ha pasado algo, en este caso, yo he elegido la 1, cual es la probabilidad de que pase el siguiente suceso, en las diferentes casos. Por si ayudara, os he hecho un diagrama.

Probabilidad de los sucesos.

Ahora, para calcular la probabilidad de cada suceso se suman las probabilidades: el cambio tiene una probabilidad de éxito de 1/3+1/3=2/3, mientras que mantener mi primera elección tiene una probabilidad de éxito de 1/6+1/6=1/3. Aquí hay una sencilla aplicación para que juegues tú mismo,  yo he jugado 20 veces manteniendo mi puerta y he ganado en 5, mientras que he jugado 20 veces cambiando mi puerta y he ganado en 13 ocasiones. Parece que mejor si cambias.

Hay una rama de las matemáticas que se dedica a estas cosas, es lo que conoce como teoría de juegos e importantes avances en este campo es por lo que le dieron el premio Nobel al John Nash,  quizá no os suene, pero si os digo que es el de la película “Una mente maravillosa”, quizá sí. Como sabéis, no existe el premio Nobel en matemáticas. Se rumorea que el tal Nobel, que fue el inventor de la dinamita, era un cornudo de cuidado, y quien se beneficiaba a su mujer era matemático. En  fin, que en su testamento no puso a los matemáticos. La principal aplicación del trabajo de este hombre es la economía, y con esta trampa, al Nash le dieron el premio Nobel en Economía. No me puedo despedir de este comentario sobre la gente importante en este campo sin mencionar a otro de los creadores de sombras, John Von Newman. Os copio un pedazo de la wikipedia: "Húngaro-estadounidense que realizó contribuciones importantes en física cuántica, análisis funcional, teoría de conjuntos, ciencias de la computación, economía, análisis numérico, cibernética, hidrodinámica (de explosiones), estadística y muchos otros campos de la matemática." Vamos, lo que se dice un listillo.


Con el anterior problema, no creo que podáis ver porque esto tiene tanta importancia en economía. Veamos con el siguiente. Uno de los problemas más famosos en este campo, del que yo no tengo ni la más pajolera idea, es el del dilema del prisionero. Como nunca he estado prisionero, pues no me siento muy identificado con esa formulación del problema, pero os cuento un semejante caso con el dilema de la máquina del café. Resulta que es normal en el norte de Europa, al menos en departamentos donde no hay todavía muchos latinos, que la máquina del café no tenga ningún dispositivo de cobro, sino que cada persona que se toma un café lo apunta en una lista y cada cierto tiempo paga. Otras veces, hay una bandeja y tú dejas el dinero.

Pongamos por caso, que llego a un lugar donde 9 personas tienen una máquina de café y yo llego nuevo. Es evidente, desde mi punto de vista, que la solución más barata para mí es no pagar el café. Eso repercutiría evidentemente en mis 9 compañeros de café, cuando repartan gastos, el café les saldrá un poquillo más caro, pero solo un poco. En este caso, mi estrategia es mucho más ventajosa que el resto de jugadores. Sin embargo, ellos que no son tontos, aunque lo parezcan por estas formas de confiar en la gente, empiezan a recelar de qué desde que llego el español, el café se ha encarecido. Así, algunos de ellos, empiezan a dejar de pagar, haciendo de este barato sistema de comprar una cafetera y café entre todos y repartir gastos, más caro (¡para los que siguen siendo honestos!) que ir a la cafetería y comprar un café. Por tanto, dejan de comprar café y todos debemos ir a la cafetería. El café, que inicialmente me hubiese costado 25 céntimos, pero que he obtenido gratis durante un cierto tiempo, ha pasado a costarme un euro y medio.  Mi solución ha resultado ser un fracaso para mí y, a la misma vez, ha conducido al fracaso al resto de mis compañeros. 

Analizando los dos juegos, el primero es competitivo, o yo gano el coche o el programa se queda el coche. En cambio, el segundo es cooperativo. En unos casos unos ganan y otros pierden, otras veces, todos ganan, y, cuando lo valorado es ser un fresco y un pillo, todos pierden. Este hombre, el John Nash, desarrollo una estrategia óptima para afrontar estos problemas donde varios jugadores deciden en juegos competitivos. Esto se conoce como Equilibrio de Nash, cada jugador no elige su acción más ventajosa, sino que elije una estrategia que no ponga en peligro la viabilidad del sistema global. Esto es muy importante en las negociaciones colectivas, por ejemplo, un sindicato puede obtener condiciones muy ventajosas para unos trabajadores, pero si esto hunde el beneficio de los jefes, estos cierran la empresa y adiós las ventajas y el trabajo. En cambio, una negociación muy buena por parte de los jefes, llevara a condiciones muy pobres para los trabajadores, que faltos de motivación, y esto afectará a los productos de la empresa, y de esta forma, a los beneficios finales de los jefes.

Soluciones muy buenas para un conjunto de jugadores que aceptan unas reglas; resultan penosas para otro conjunto de jugadores si no aceptan las reglas. En mi opinión, esto es lo que hace que las políticas económicas de izquierdas o de derechas no sean buenas o malas de por sí; algunas son imposibles si no se aceptan las reglas comunes para optimizar al conjunto y no al jugador.

El primer día dices: "¡Qué tontos son estos guiris!", tras un tiempo te dices: "Son una raza superior".